Zero Knowledge Proof

The digitisation of many processes and the constant technological evolution bring with them many benefits, but also new possibilities for cyber-attacks. Many companies nowadays collect a large amount of data that helps them to improve their marketing mechanisms, products and services, making them more prone to constant attacks. That is why in this article we will explain how Zero Knowledge Proof (ZKP) allows to protect confidential data and increase privacy by using mathematical calculations.

More security is needed

Data is becoming more and more important every day and at the same time, we find an exponential increase of IoT devices in our world. This is why there is a need for a security system that can guarantee the safety of data transmission at all times. Industry 4.0 will lead to an unimaginable number of devices connected to the Internet, such as sensors, smart cars, detection cameras, etc.... All this is a big step towards the Internet of Things (IoT) where the main goal is to improve the quality of our lives. The problem is that all the data will be exposed to another large number of threats if we are not able to use a secure data encryption mechanism.

In the IoT sector, machine-to-machine or machine-to-human transactions require speed and scalability at increasingly demanding levels and need to maintain the privacy of sensitive information. There are already various methods for scalability of IoT devices and methods to increase the speed of transactions and processing, however, not as much effort has been made to ensure data privacy.

ZKP

The concept of Zero Knowledge Proof was originally published by MIT in 1985. Zero Knowledge Proof is a mathematical technique by which the veracity of data can be verified without revealing the information itself. This article will not go into detail on the mathematical explanation behind the mechanism, but it is interesting to clarify two very important concepts:

Elliptic curve cryptography

Elliptic curve cryptography consists of a set of points satisfying an elliptic curve equation, which is easy to compute but very difficult to reverse. It is a variant of asymmetric or public key cryptography and is based on elliptic curves.

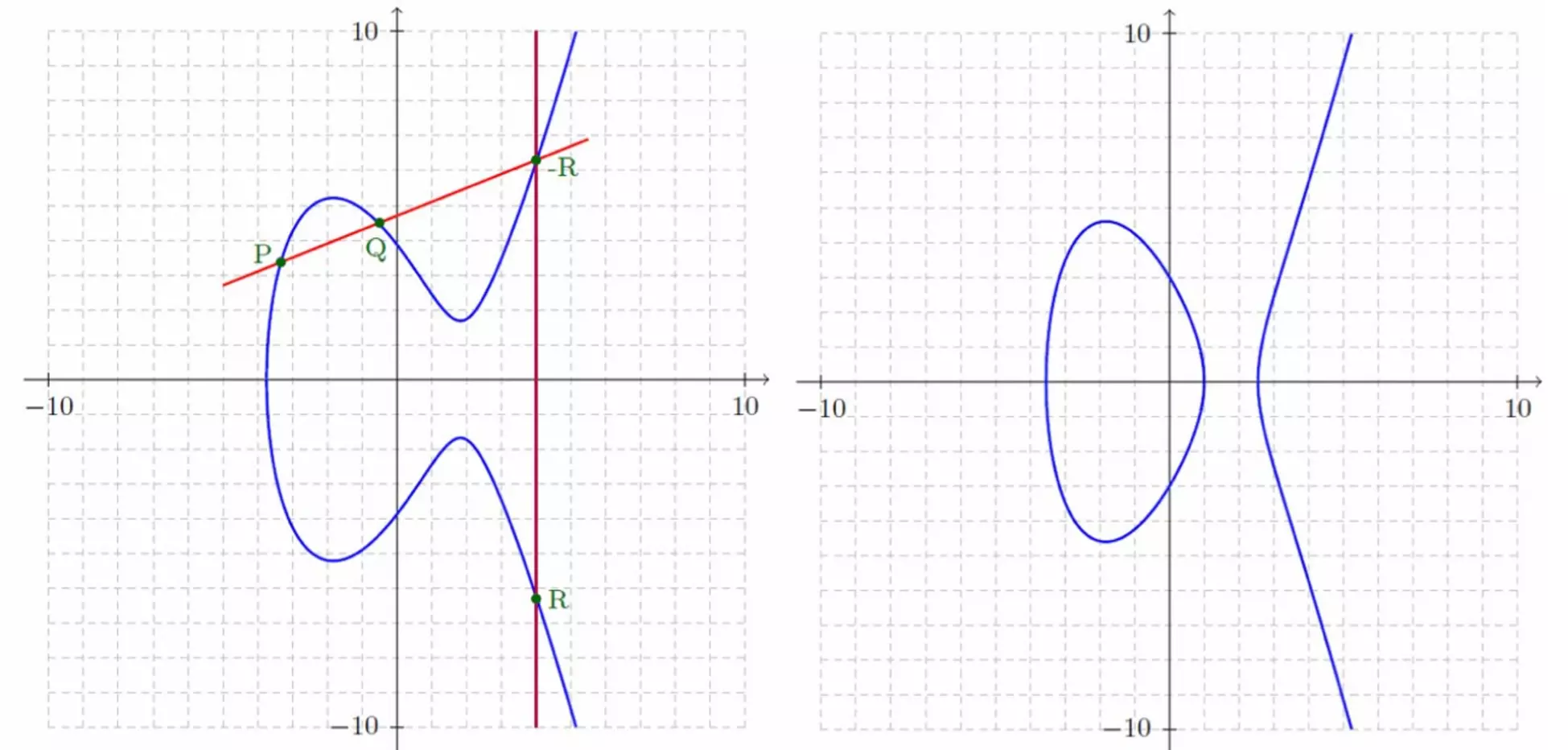
An elliptic curve is a set of points that satisfy a specific mathematical equation. The equation for an elliptic curve looks like this:

𝑦 ! = 𝑥" + ax + b

So we can say that it is very easy to create an ECC key, but breaking it is practically impossible. The main difficulty lies in the infeasibility of calculating the discrete logarithm of a random elliptic curve element with respect to a publicly known base point. This is known as the "Elliptic Curve Discrete Logarithm Problem (ECDLP)".

Basically it is the existence of a private key and a public key. The private key is used to encrypt the data into a hash and that hash can be used to verify the owner. A fairly clear example is explained in the article published by ISA Manipal.

Quadratic residuals

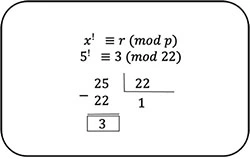
A quadratic remainder, in mathematics, is the number that leaves the square of any other number when divided by another number called the modulus. In a more formal way it can be said that 'The integer r is a quadratic residue of a prime p if there exists an integer x such that x squared leaves residue r in the division x^2 / p. The equation is such that: 𝑥! ≡ 𝑟 (𝑚𝑚𝑜𝑑 𝑝)

Let's give an example to make it clearer: If we say that 3 is a quadratic remainder of modulus 22, it means that if we choose a number x such as x = 5, dividing the square of x (25) by the modulus (22), it should give a remainder of 3.

Simple explanation of the ZKP for your children

Instead of giving a mathematical or theoretical explanation, it will be better to understand what this method consists of with an example published by Jean Jacques and Louis Guillou in a report called "How to Explain Zero-Knowledge Protocols to your children".

Let's imagine that there are two people (A and B) in a cave, and inside the cave there is a door that connects C and D. Person A knows the combination that has to be entered in the door to open it and wants to demonstrate it to B, but without telling him the key, so he has to enter it:

1. First, person A starts walking towards either side of the cave (C or D).
2. Once person A is no longer in sight, B goes to the position from where person A started and can see both paths.
3. Person B can now instruct A to exit in lane C or lane D.
4. Because A knows the key, he will use it to open the secret door and exit through the lane B told him.
5. B may not be convinced because it could have been luck as he had a 50% chance of guessing the key correctly.
6. So person B decides to repeat it 25 times or any number. If this test is repeated several times, the probability of finally guessing the key would be very low.
7. This allows B to verify that A knows the key without revealing the information (the key).

Main properties

Integrity	If the information provided is true, the verifier will be able to verify the veracity of that information over and over again.
Solidity	In case the information is false or erroneous, the verifier will know that the information is directly false.
Zero knowledge	In case the information is true, the verifier will not know the information itself, it will simply know if it is true or false, nothing else.

ZKP types: zk-SNARKs vs zk-STARKs

There are currently two types of ZKP that are highly recognised. Firstly zk-SNARK which were the first tests and are used in projects such as Zcash, although they have caused problems such as "creating coins out of thin air" and secondly zk-STARK which is an improvement on SNARKs.

• zk-SNARK: "Zero Knowledge Succinct Non-Interactive Argument of Knowledge" it is a zero-knowledge type of proof, so ZKP is not the same as zk-SNARK, but zk-SNARK is built on ZKP. By referring to the term "non-interactive", it means that there is no constant exchange between the demonstrator and the verifier. This type of ZKP requires more computational power, higher cost and greater vulnerability to quantum attacks.
• zk-STARK: "Zero Knowledge Scalable Transparent Argument of Knowledge" this is a major improvement on zk-SNARK and unlike SNARK, there is a constant trade-off to get the verifier to be convinced. zk-SNARK required a trusted configuration phase, whereas zk-STARK does not rely on such a configuration but uses publicly verifiable randomness. In addition, they are more scalable in terms of both speed and computational size, i.e. they are not as complex as zk-SNARKs, where complexity can sometimes cause problems, and finally, they are more resistant to quantum attacks.

We are still on the road to privacy

It is clear that not everything can be perfect, and in some ways the use of zero-knowledge proofing is not 100% perfect. Although the protocol allows for high levels of anonymity, security and privacy, it also has some drawbacks. For example, the impossibility to guarantee that the information is 100% truthful. That is, as explained above, if the interactions between tester and verifier are repeated many times, there comes a point where the probability of a random hit is extremely low, but it can never reach zero. On the other hand, the computational power required is greater than that of other protocols, as well as the size of the time required to perform it.

However, encryption algorithms are continually being improved to reach a turning point where they can be used consistently and bring with them a multitude of benefits for secure and anonymous data transmission. It is already being applied in the military sector, to secure communications to prevent enemies from decrypting them, or in the healthcare sector, for medical records, in projects such as ZCash, Monero and IoT devices with protocols such as Crowdpatching, which applies security patches in the updates of these devices.